Blog Matemático : novembro 2016

domingo, 13 de novembro de 2016

Operações com número complexos na forma algébrica " z = a + bi"

Vamos demonmstar operações com números complexos na forma algébrica através de exemplos :

Exemplo 1 " Soma"

Considere os seguintes números, 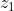$z_{1}$ e $z_{2}$ :

$z_{1}= 2 + i$

$z_{2}= -4 + 2i$

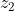Queremos efetuar a soma entre estes dois números complexos na forma algébrica $(z_{1} + z_{2})$

O Exemplo será resolvido aqui em baixo

$(z_{1} + z_{2}) = (2 + i)+(-4+2i) = 2 + i - 4 +2i =(2-4) + (1+2)i = -2 + 3i$

Por os dois números complexos entre parenteses ,depois deixar o prímeiro número complexo igual mas sem parentesis e efetuar as regras da adição entre a tal soma e o segundo número complexo, depois juntar a parte real toda em primeiro e a partes imaginárias "com i" com a soma dos coeficientes entre parenteses e o i.

Exemplo 2 " Diferença"

Considere os seguintes números, 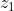$z_{1}$ e $z_{2}$ :

$z_{1}= 2 + i$

$z_{2}= -4 + 2i$

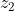O Exemplo será resolvido aqui em baixo

$(z_{1} - z_{2}) = (2 + i)-(-4+2i) = 2 + i + 4 -2i =(2+4) + (1-2)i = 6 -i$

Exemplo 3 " Mutiplicação"

Considere os seguintes números, 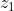$z_{1}$ e $z_{2}$ :

$z_{1}= 2 + i$

$z_{2}= -4 + 2i$

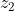O Exemplo será resolvido aqui em baixo

$(z_{1} \times z_{2}) = (2 + i)(-4+2i) = 2 \times (-4) + (2\times 2)i + (1\times -4)i + (i\times 2i) = -8 + 4i +-4i + 2i^2 =-8 + 2\times -1 = -8 -2 = -10$

Dados Importantes :

$i^2=-1$

Para quem não sabe como se efetua uma mutiplicação entre binómios

$(a+b)(c+d) = (a\times c) + (a\times d) + (b\times c) + (b\times d)$

Casos Notáveis :

Quadrado do Binómio :

$(a+b)^2= a^2 + 2ab + b^2$

Diferença de Quadrados :

$(a+b)(a-b)= a^2 - b^2$

Exemplo 4 " Divisão"

Considere os seguintes números, 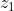$z_{1}$ e $z_{2}$ :

$z_{1}= 2 + i$

$z_{2}= -4 + 2i$

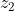O Exemplo será resolvido aqui em baixo

$(\frac{z_{1}}{z_{2}}) = \frac{2+i}{-4+2i} = \frac{(2+i)(-4-2i)}{(-4+2i)(-4-2i)}= \frac{-8-4i-4i-2i^2}{(-4)^2 + (-2)^2} = \frac{-6-8i}{16 + 4}= \frac{-6-8i}{20} =-\frac{3}{10} - \frac{2}{5}i$

sábado, 12 de novembro de 2016

Exercício de Complexos : Real , imaginário, Conjugado e Simétrico

Exercício Simples introdução aos números Complexos

Complete a Seguinte Tabela

Número Complexo (z)	Re (z)	Im (z)	Conjugado ()	Simétrico (-z)
z = 3 + 2i
		-6		.-z = -2 + 6i
z = + i
	3		z = 3 - 2i
		-3		-z= 2 + 3i

Números Complexos Introdução : Número Complexo, conjugado e simétrico

Os Números Complexos são representados na forma

onde P é o afixo de coordenadas (a,b), sendo o eixo dasa abcissas (x) o eixo dos Reais "Re (z)", sendo Re (z) = a e os eixos dos imaginários (y) "Im (z)", sendo Im (z) = b

Exemplo :

Conjugado do Número Completo "

O Conjugado do Número do número complexo representa se por

, e a diferença que tem do número complexo é que o número imagínário " Im (z)" troca de sinal, ou seja é o simétrico ficando

Representação geométrica do Número Complexo e o seu conjugado

Simétrico do Número de Complexo :

O Simétrico do número complexo "

" troca - se o sinal do número imaginário e do número real , ficando

Representação Gráfica do Número Complexo e o seu simétrico

sexta-feira, 11 de novembro de 2016

Matemática - Ensino Primário : Mutiplicar e Dividir números inteiros e decimais por 0.001,0.01,0.1,10,100,1000

Para mutplicar um número qualquer por 10 (que é a mesma coisa que dividir por 0,1), adiciona . se 1 zero (0) a esse número ou avança se uma casa decimal

Exemplos :

1245 x 10 = 12450 = 1245 / 0.1

12,3 x 10 = 123 = 12,3/0,1

1,47 x 10 = 14,7 =1,47/0,1

Para mutiplica um número qualquer qualquer por 100 ( que é a mesma coisa que dividir por 0,01) adiciona - se 2 zeros (0) a esse número ou avança se duas casas decimais

Exemplo :

786 x 100 = 78600 = 78,6 / 0.01
5,67 x 100 = 567 = 5,67 / 0,01
8,21 x 100 = 821 = 8,21/0,01

Para se mutiplicar um número qualquer por 1000 ( que é a mesma coisa que dividir por 0,001) adiciona .- se 3 zeros (0) ou avança se três casas

Exemplo :

1489 x 1000 = 1489000 = 1489 / 0,001
1,234 x 1000 = 1234 = 1,234 / 0,001
364,7x1000 = 364700 = 364,7/0,001

Para se dividir um número qualquer por 10 (que é a mesma coisa que mutiplicar por 0,1) retira se um zero ou recua se a virgula a uma casa

Exemplos

1820/10 = 182 = 1820 x 0,1

456/10 = 45,6 = 456 x 0,1

88,7 / 10 = 8,87 = 88,7 x 0,1

Para se dividir um número qualquer por 100 ( que é a mesma coisa que mutiplicar por 0,01) tira se dois zeros ou recua se a virgula a duas casas

Exemplos :

1654 / 100 = 16,54 = 1654 x 0,01
24830 / 100 = 248,3 = 24830 x 0,01
8200000/100 = 82000 = 8200000 x 0,01

Para se dividir um número qualquer por 100 ( que é a mesma coisa que por mutiplicar por 0,001) tira se três zero ou recua se a virgula a três casas

Exemplos :

1589000/1000 = 1589 = 1589000 x 0,001
4500/1000 = 4,5 = 4500 x 0,001
6,32 /1000 = 0,00632

Equações Racionais MUITO SIMPL ; Como Resolver ?

Encontra se aqui um exemplo muito simples : esta expressão da esquerda tem domínio

ou seja

Para resolver esta equação temos que considerar a parte de cima igual a 0, ou seja o numerador igual a 0 e o denominador diferente de 0, ou seja, não há números a divir por 0

Assim fica :

Resolvendo fica :

Sendo a única solução - 3

Regras dos Logaritmos "12º Ano"

Os logaritmos representam - se na forma de

sendo o inverso das potências ou seja

, sendo a a base o b o resultado e x o expoente , logaritmos com base 10 representam - se apenas por

e logaritmos com base do número de neper "e" representam - se por

Exemplos :

<=>

Regras logarítimicas

Começamos pela regra de adição de logaritmos :

Quando adicionamos logaritmos com a mesma base e número total diferente, mutiplicam - se esses números totais, ficando o logaritmo na mesma base so que com a mutiplicação entre os dois "números totais"

~Exemplo

A regra de subtração de logaritmos

Na subtração de logaritmos com a mesma base e números totais e diferentes, mantém se as bases e divide - se os números totais

Exemplo :

Na regra de potenciação de logaritmos

Na regra de potênciação de logaritmos o expoente da potência so número total passa para mutiplicar e fica o expoente a mutiplicar pelo logaritmos

Exemplo :

Na regra de Mudança de base dos logaritmos